红黑树插入流程详解

红黑树平衡性原则

• 根结点是黑色（有的版本对根结点的颜色没有强制要求）
• 所有节点只能是红色或者黑色
• 所有的叶子节点都是黑色，这里说的叶子结点是 NULL 叶子结点
• 如果一个节点是红色的，那么它的两个孩子只能是黑色的（即不能同时出现两个连续的红色节点）
• 从任意的一个节点出发，到它的所有叶子节点路径上都包含相同数量的黑色节点

另外，看似使用全部黑色的节点也符合红黑树的规则，但是实际上它已经失去了红黑树的优势，和普通的 BST 没有啥区别了。

红黑树的插入修复

在节点插入过程中，根据红黑树平衡性原则可以发现，只有 parent 节点是红色的时候才会出发平衡性修复，具体的分为以下几种情况：

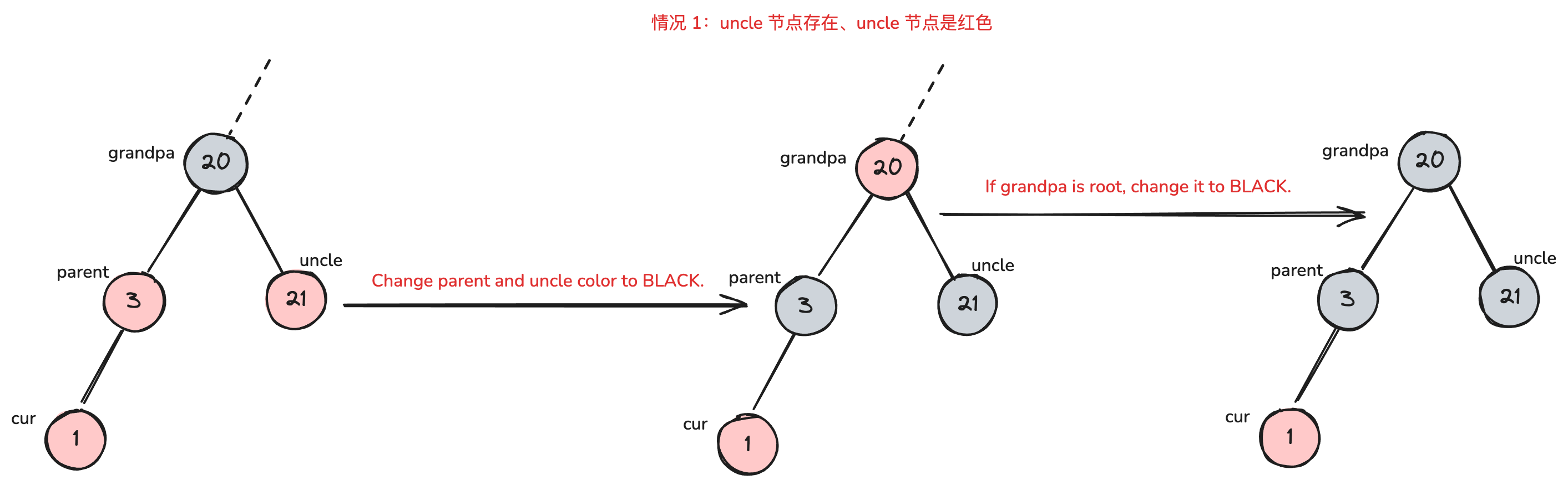
情况 1. uncle 节点存在，并且 uncle 节点是红色

• 修复方法：
  • grandpa 节点从黑色变为红色，parent 和 uncle 节点由红色变为黑色
  • 如果此时 root 节点变成了红色，直接给染黑就行
  • 修复过程不需要任何旋转操作

情况 2. uncle 节点不存在，或者 uncle 节点存在并为黑色

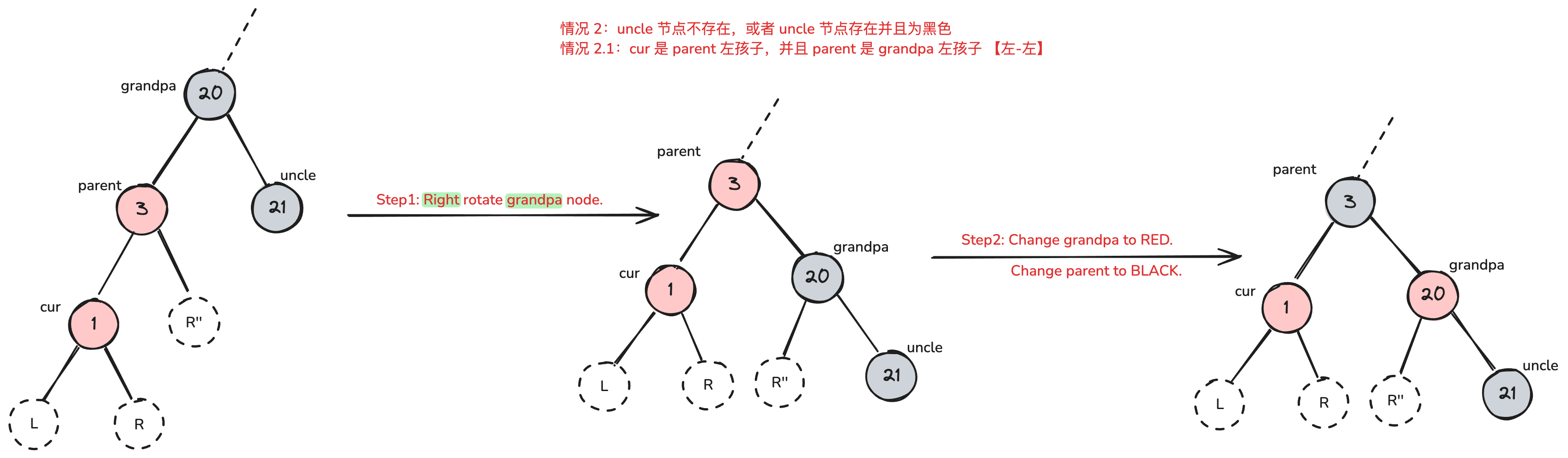
• 情况 2.1 【左-左】 cur 是 parent 左孩子，parent 是 grandpa 左孩子
  • 修复方法：grandpa 右旋并染为红色，parent 染色黑色
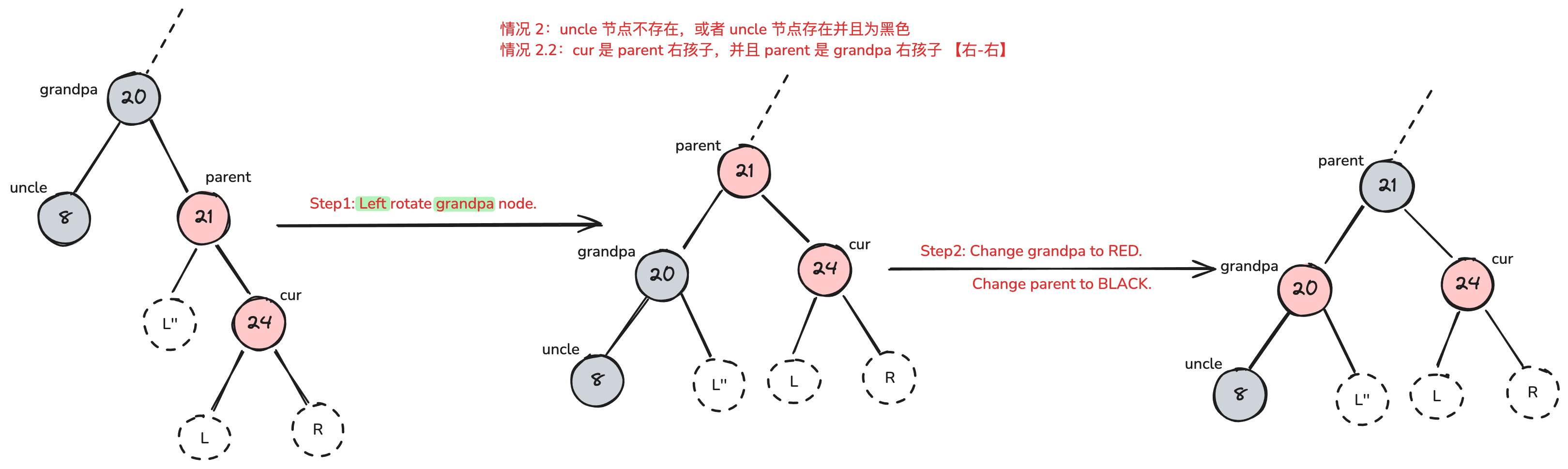
• 情况 2.2 【右-右】 cur 是 parent 右孩子，parent 是 grandpa 右孩子
  • 修复方法：grandpa 左旋并染为红色，parent 染色黑色
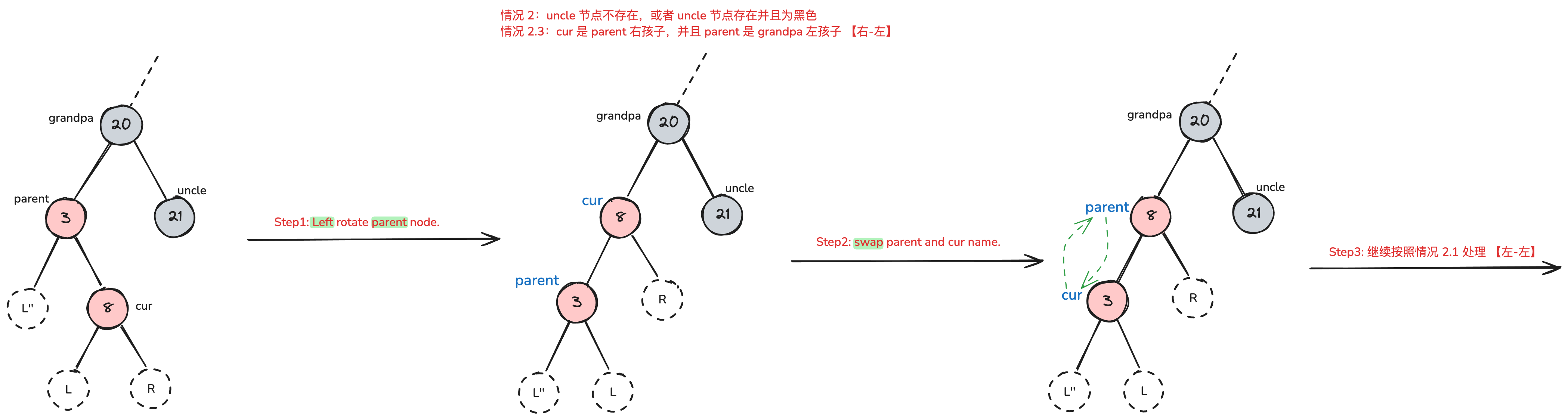
• 情况 2.3 【右-左】 cur 是 parent 右孩子，parent 是 grandpa 左孩子
  • 修复方法：parent 左旋，将 parent 与 cur 节点名称互换，并继续按照情况 2.1 处理
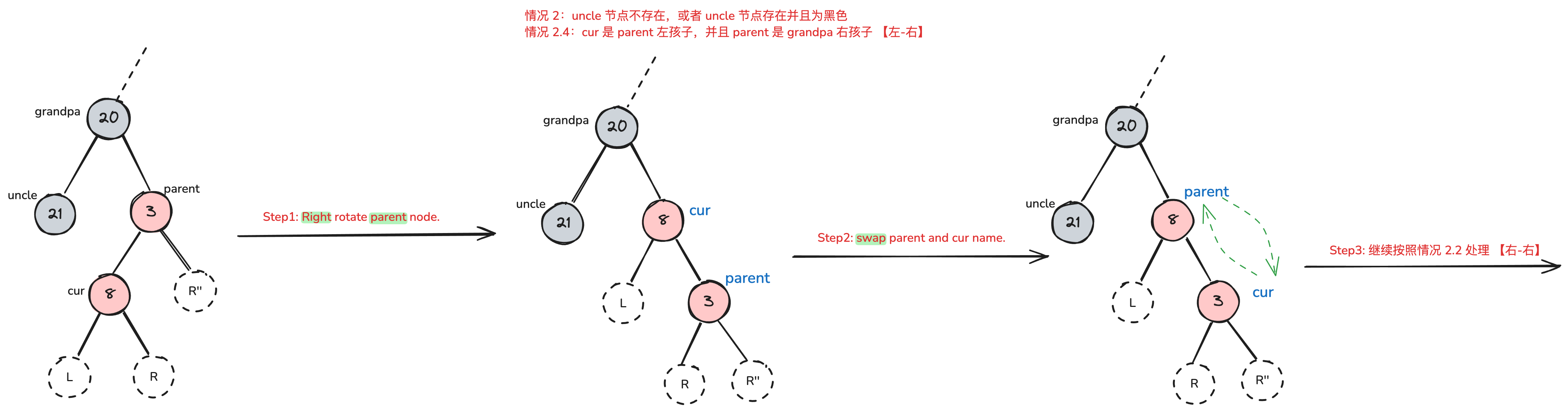
• 情况 2.4 【左-右】 cur 是 parent 左孩子，parent 是 grandpa 右孩子
  • 修复方法：parent 右旋，将 parent 与 cur 节点名称互换，并继续按照情况 2.2 处理

图例

情况 1. uncle 节点存在，并且 uncle 节点是红色

• 修复方法：
  • grandpa 节点从黑色变为红色，parent 和 uncle 节点由红色变为黑色
  • 如果此时 root 节点变成了红色，直接给染黑就行
  • 修复过程不需要任何旋转操作

情况 2. uncle 节点不存在，或者 uncle 节点存在并为黑色

• 情况 2.1 【左-左】 cur 是 parent 左孩子，parent 是 grandpa 左孩子
  • 修复方法：grandpa 右旋并染为红色，parent 染色黑色
• 情况 2.2 【右-右】 cur 是 parent 右孩子，parent 是 grandpa 右孩子
  • 修复方法：grandpa 左旋并染为红色，parent 染色黑色
• 情况 2.3 【右-左】 cur 是 parent 右孩子，parent 是 grandpa 左孩子
  • 修复方法：parent 左旋，将 parent 与 cur 节点名称互换，并继续按照情况 2.1 处理
• 情况 2.4 【左-右】 cur 是 parent 左孩子，parent 是 grandpa 右孩子
  • 修复方法：parent 右旋，将 parent 与 cur 节点名称互换，并继续按照情况 2.2 处理