初识并查集

并查集 DSU 详细解释可以参考 OI DSU, 它主要适用于这些场景（GPT）:

• 图的连通性问题
  • 并查集可以用来判断图中两个节点是否能够联通，即判断两个节点是否属于同一个集合
  • 判断图是否联通
  • 求解图中联通分量的数目
• 最小生成树算法
  • Kruskal 算法，通过并查集判断添加的边是否会形成环，从而构建最小生成树
• 图的动态连通性
• 确定无向图的环
• 划分问题：将一组元素划分为不相交的集合，并查集可以跟踪每个元素所属的集合
• 等价关系
• 邻接矩阵的缩点
• 不相交集合的合并
• 路径压缩
• 二维数组中的区域标记

本文主要是记录并查集是如何去解决图的连通性问题。

题目

Reference 1697. 检查边长度限制的路径是否存在

给你一个 n 个点组成的无向图边集 edgeList ，其中 edgeList[i] = [ui, vi, disi] 表示点 ui 和点 vi 之间有一条长度为 disi 的边。请注意，两个点之间可能有超过一条边 。

给你一个查询数组 queries ，其中 queries[j] = [pj, qj, limitj] ，你的任务是对于每个查询 queries[j] ，判断是否存在从 pj 到 qj 的路径，且这条路径上的每一条边都严格小于 limitj 。

请你返回一个布尔数组 answer ，其中 answer.length == queries.length，当 queries[j] 的查询结果为 true 时， answer 第 j 个值为 true ，否则为 false。

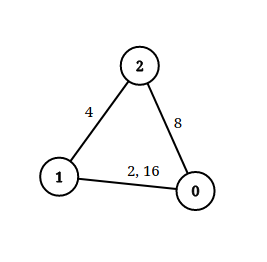
输入：n = 3, edgeList = [[0,1,2],[1,2,4],[2,0,8],[1,0,16]], queries = [[0,1,2],[0,2,5]]

输出：[false,true]

解释：上图为给定的输入数据。注意到 0 和 1 之间有两条重边，分别为 2 和 16。 对于第一个查询，0 和 1 之间没有小于 2 的边，所以我们返回 false 。 对于第二个查询，有一条路径（0 -> 1 -> 2）两条边都小于 5 ，所以这个查询我们返回 true 。

代码

代码分析