1074.元素和为目标值的子矩阵数量

题目

原题 1074.元素和为目标值的子矩阵数量

解题

这个题目直接使用暴力方法竟然能 AC…

暴力思路是：先计算出二维数组的前缀和并存储下来，然后使用 O(n^4) 枚举所有可能出现的子矩阵位置（枚举左上角的坐标和右下角的坐标即可），然后通过存储的前缀和去计算出每个子矩阵的 sum，判断是否符合 target。

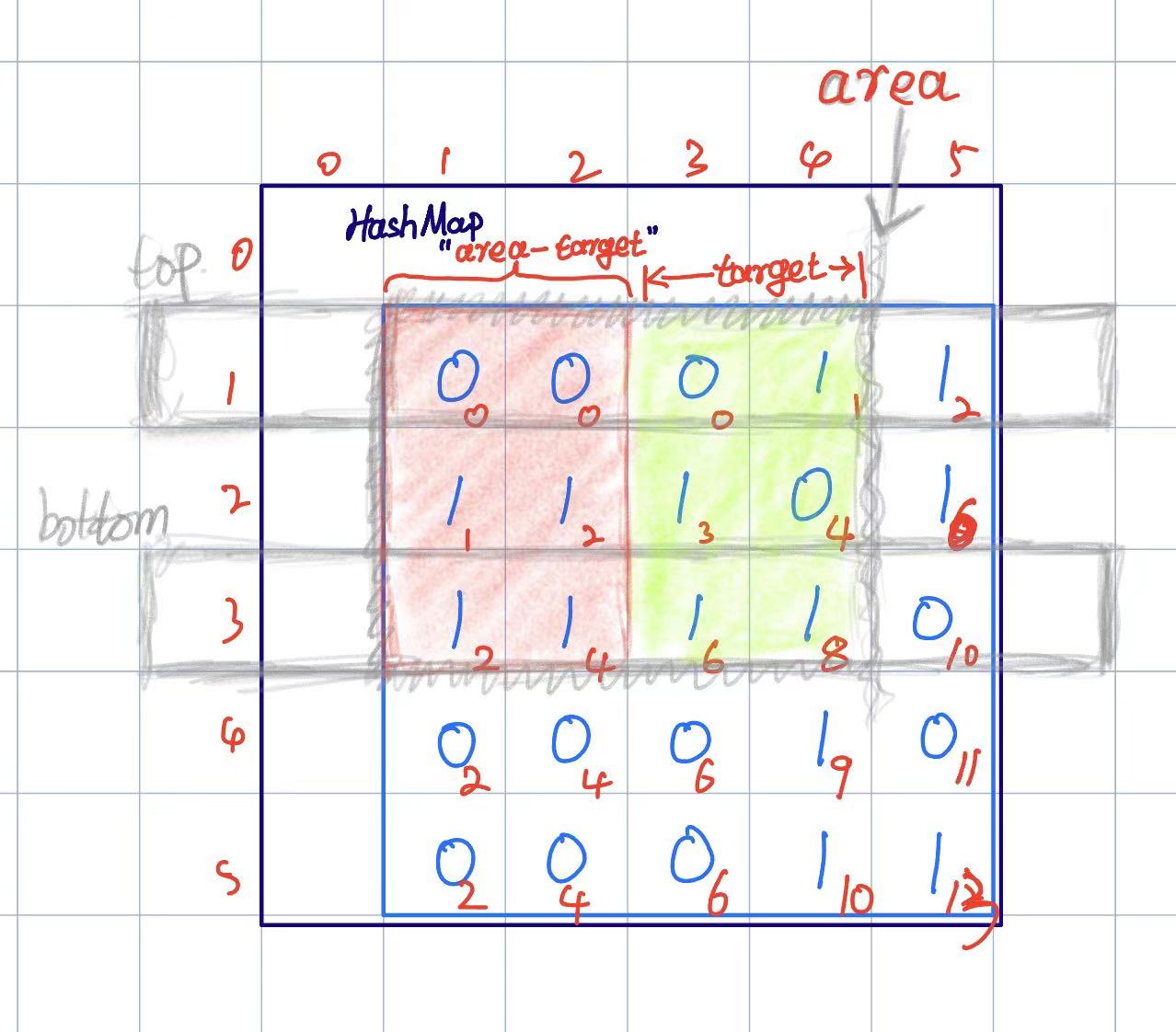
现在需要探讨的是使用 HashMap 去优化这个 O(n^4) 的遍历过程，可以考虑先确定子矩阵的上下界，上下界限固定后，可以通过移动子矩阵的右边界，并使用 HashMap 缓存右边界移动过程中的子矩阵 area 面积大小，这样就能够通过 HashMap 记录的 area 面积历史去确定是否存在子矩阵的面积为 target。具体的可以直接看图理解：

具体的代码如下：

public int numSubmatrixSumTarget(int[][] matrix, int target) {
    int[][] sum = new int[matrix.length+1][matrix[0].length+1];
    int res = 0;
    // 计算前缀和
    for (int i=1; i<sum.length; i++){
        for (int j=1; j<sum[0].length; j++){
            sum[i][j] = matrix[i-1][j-1] + sum[i-1][j] + sum[i][j-1] - sum[i-1][j-1];
        }
    }

    // 枚举上边界
    for (int top = 1; top < sum.length; top++){
        // 枚举下边界，上下边界均为包含状态，即范围是 [top, bottom]
        for (int bottom = top; bottom < sum.length; bottom++){
            // 建立临时 map, 存储记录遍历 right 边界时面积为 area 的子矩阵出现的次数
            // map 中存储的面积实际上都是以最左侧边界线为起点的矩阵
            HashMap<Integer, Integer> map = new HashMap<>();
            // 从最左侧开始遍历
            for (int right=1; right<sum[0].length; right++){
                // 计算当前 right 边界与最左侧边界形成的“大子矩阵”面积
                int area = sum[bottom][right] - sum[top-1][right];
                // 符合 target 则 res++
                if (area==target)
                    res++;
                // 判断这个“大子矩阵”内部是否有“小子矩阵”符合 target
                // 也就是说，如果有小子矩阵符合 target, 那么 map 中一定存在 area-target 这个面积的另一个子矩阵
                if (map.containsKey(area-target)){
                    res += map.get(area-target);
                }
                // 更新 map
                map.put(area, map.getOrDefault(area, 0)+1);
            }
        }
    }
    return res;
}